DreamCoder and Neural Program Induction

While going through my bookmarks on Twitter, I found this brilliant paper that introduced me to so many new ideas and directions of machine learning research. I am writing this to log them here, and to point myself/others to in the future.

• DreamCoder $\rightarrow$ wake-sleep Bayesian Program Induction.
• Learning a new task $\implies$ search for a program that solves it

Some definitions:

• Neural Program Synthesis: Find or guess a program that solves the problem. We can then modify or read the program generated.
• Neural Program Induction: Infer what the program will do, and do it (but do not explicitly generate the program) (more like a latent space thing)

The problem now is to generate program $\rho_x,$ given task $x\in X$ and a prior distribution of programs $L.$ So we need to maximize probability $P(\rho_x| x, L).$

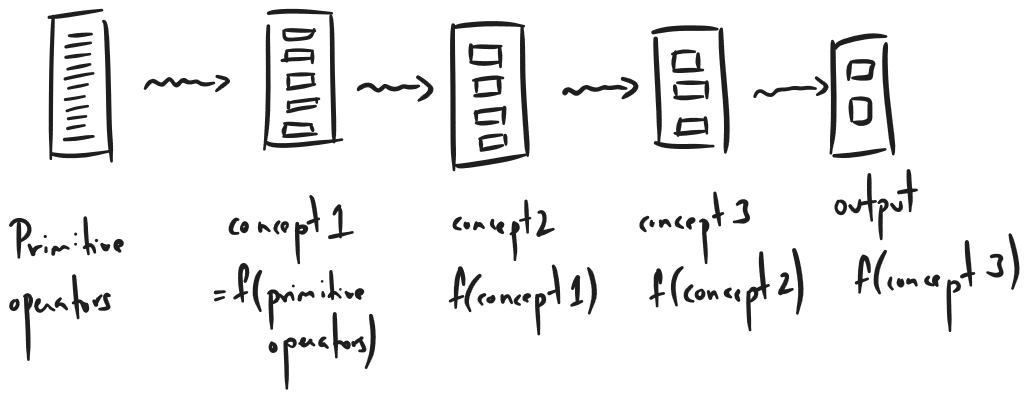
Initially, $L$ would just be a bunch of primitive operators like $+,-\times,\div,$ modulo, if, and, or, etc. Performing a program search using just these would take ages, just like how trying to use NAND gates for everything would take ages (I actually don’t know if this is true, I just like the analogy).

Therefore, we add to $L$ by learning functions that are composites of the basic operators. This reduces the size of things we need to search from.

In the waking phase, choose $\rho_x$ that maximizes

\[P[\rho|x, L] \propto P[x|\rho]\cdot P[\rho|L],\]

and in the sleep phase, we expand $L$ with a routine that maximizes

\[P[L]\prod_{x\in X}\max_{\rho_i}P[x|\rho]\cdot P[\rho|L],\]

where $x\in X$ means that we iterate over all tasks and $\rho_i$ are all refactorings of $\rho_x$ when $L$ is updated. Now we train $Q(\rho|x)\approx P[\rho|x,L],$ where $x\sim x$(‘replay’) or $x\sim L(‘fantasy’). And this is what they term as dreaming in sleep.

The way I understand the $P[\rho|L]$ term is that we maximize the probability of generating a program from the library and this happen if we choose simpler programs from the learned concepts rather than the primitives.

• Long programs are more likely to be made of primitives $\rightarrow$ more likely to overfit training samples and not be a general solution. (at least that’s the intuition)

Aside: The ARC challenge by Francois Chollet

This approach still doesn’t do classical perception tasks that large neural nets + lots of good quality data do. A good problem is to bridge the gap.

Some New Ideas are here needed!!

---