Implementing Automatic Differentiation in Pure Python

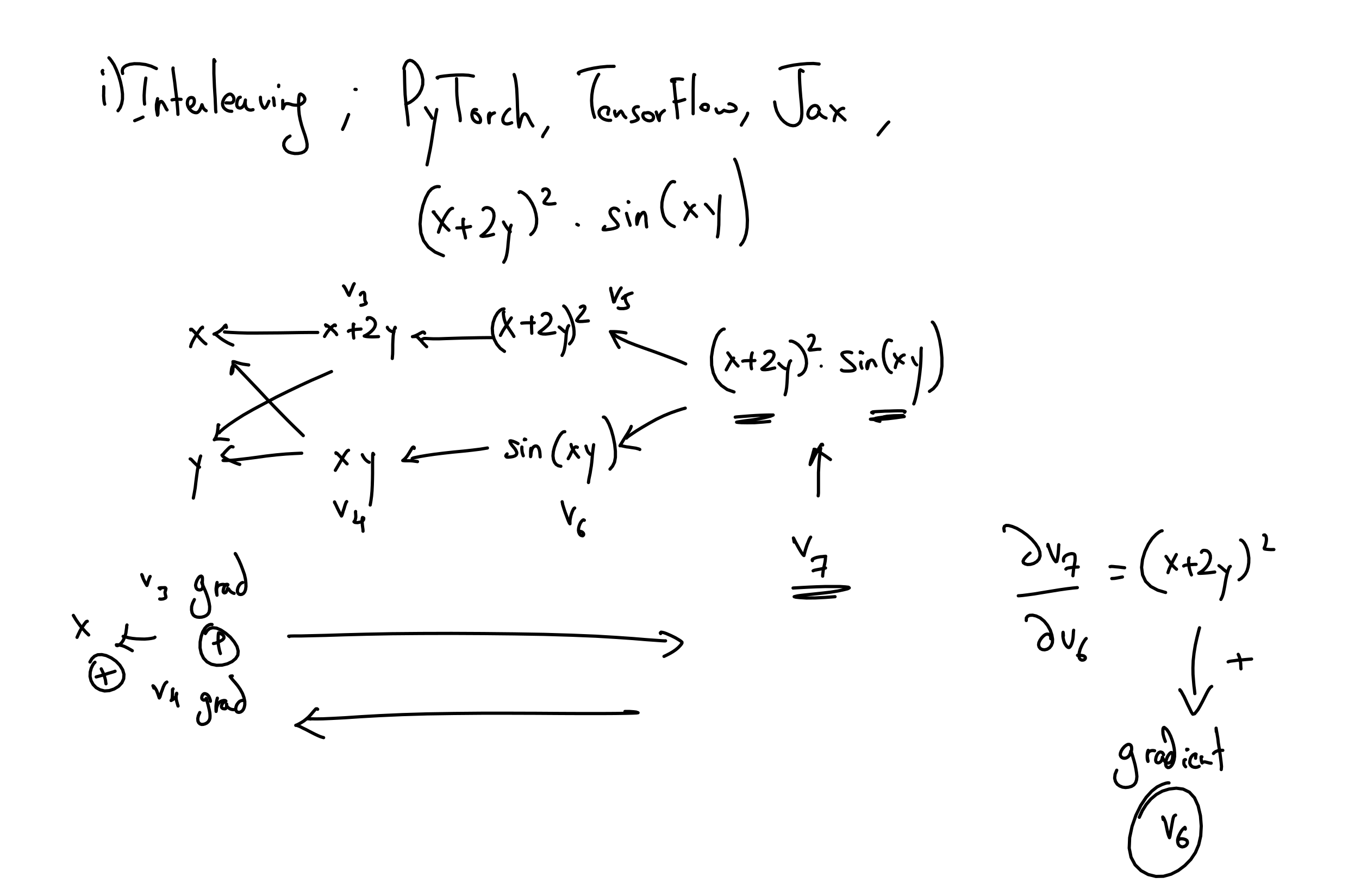
A recording of me explaining and implementing automatic differentiation in pure Python. I start with some mathematics of forward and reverse mode autodiff and then implement interleaved forward mode autodiff. Then I explain how to use Dual Numbers and implement forward mode autodiff using Dual Numbers. Finally, I construct a computation graph and perform a topological sort to achieve reverse mode autodiff.

Resources

• Wikipedia - Automatic Differentiation
• Backprop is not just the chain rule by Tim Vieira on Graduate Descent
• Evaluating $\nabla f(x)$ is as fast as $f(x)$ by Tim Vieira on Graduate Descent
• How to test gradient implementations by Tim Vieira on Graduate Descent
• micrograd by Andrej Karpathy (the greatest ever)

Update: ever since I published my video, I have had many interesting discussions with people about autodiff and I found these links to be very useful in improving my understanding of autodiff. I’m linking them below so that many more can learn from them.

• PyTorch Autograd Explained by Elliot Waite
• Automatic Differentiation by Justin Domke
• Introduction to Automatic Differentiation
• On backpropagation for neural networks by Artem Kirsanov

Code

• fmadinterleaved.py: implementation of forward mode autodiff by straightforward interleaving
• dnexample.py: an example implementation of dual numbers and usage for finding derivatives
• fmaddual.py: implementation of forward mode autodiff using dual numbers
• rmad.py: implementation of reverse mode autodiff by building a computational graph
• ftest.py: code to test whether numbers generated are correct

Notes